The problem of finding significant effects in fractional factorial experiments is viewed as a variable selection problem. In this study, various forward selection and backward elimination strategies are compared. The smallest effects are pooled for error, and p-values are found by Monte Carlo simulations. Possible independent degrees of freedom for error are also utilized. To increase the power, a so-called realistic model strategy is presented.
A multiresponse generalization of the forward selection procedure is developed. In the generalized procedure, collinear responses are effectively handled by successive principal component decompositions. For instance, the number of response variables can greatly exceed the number of observations.
The underlying and more general concepts for hypothesis testing in multivariate multiple regression models are also treated. In particular, a geometrical interpretation of the classical tests of the relation between two sets of variables is presented. The traditional tests are formulated geometrically as resampling tests where rotation matrices play the same role as permutation matrices in permutation tests. The distributions of generalized test statistics can be formulated in a similar way.
To estimate the regression parameters in designed multiresponse experiments, many chemometricians would like to use PLS2. It is shown that PLS2 applied to orthogonal explanatory variables is identical to reduced rank regression. In fractional factorial designs this means that PLS2 gives identical results to ordinary least squares applied to principal components of the response variables.
Scientists and technologists are often interested in modeling relationships between one or more response variables and a number of predictor variables. In situations where knowledge of the underlying physical mechanism is lacking such models have to be based on empirical studies. When the predictor variables can be manipulated, it is always useful to vary them systematically according to an experimental design.
However, in complex situations we can never find the true model. The nature of the experimental learning process is iterative and each new experiment increases our knowledge. Indeed, it is very important to use a strategy that will give us the most important and useful information first. When there is a large number of potentially influential variables, the initial experiments should therefore be used to identify the most important variables. For this purpose, two-level fractional factorial designs are extremely useful. These designs are also known as screening designs.
To draw conclusions from experimental data, statistical tools are very useful. Although, in many cases, we get much information by just looking at the data. The role of statistics is to get as much information as possible from a limited number of experimental runs. Statistical methods are needed because experimental error (noise) is present in all types of empirical studies. In particular, statistical hypothesis tests can answer questions about whether we can rely on observed relationships.
This thesis treats the problem of identifying important variables in fractional factorial design by hypothesis testing techniques. Since replicates are not performed, this leads to special statistical problems. Today, problems related to hypothesis tests can often be solved by extensive use of computer power. When it is impossible to calculate p-values analytically, we can perform so-called Monte Carlo simulations. Using Monte Carlo simulations this thesis improves existing uniresponse methods for fractional designs (PAPER 1 and PAPER 3).
Modern instruments often measure many variables and there is often a high degree of collinearity among the variables. However, multiresponse tests for fractional design have, until now, been non-existent. The final paper (PAPER 5) of this thesis develops multiresponse methodology for such experiments. The special problems concerning collinear data are also handled. The underlying and more general concepts for hypothesis testing in multivariate multiple regression models, is treated in PAPER 4.
Below, we refer to the multivariate multiple regression model
where n is the number of observations. Here 
is the vector of
intercept terms and 
is the matrix of the other regression parameters.
The matrix 
consist of random disturbances whose rows are
uncorrelated multinormal with zero mean and a common covariance matrix.
This model is often underlying many of the most common statistical methods.
Note that models with categorical design variables (MANOVA, ANOVA) can
also be written on this form. It is, however, very important to distinguish
between cases where 
is designed and cases where is observed.
First, consider the uniresponse cases (p=1) with an observed and a
relatively large number, k, of explanatory variables. The performance of
the ordinary least squares estimate (OLS) is often very poor. This can be
explained by too many unknown parameters in the model (overfitting) or near
collinearity in the data. This problem can be handled by several estimation
methods. So far, principal component regression (PCR), partial lest squares
regression (PLS), ridge regression (RR), and variable subset selection (VSS)
are the most common methods
(See Martens and Næs (1989) and Frank and Friedman (1993) )
The methods PCR, PLS and RR can be viewed as methods that mainly focus
on linear combinations of the X-variables with high sample variance.
PCR is based directly on the singular value decomposition (SVD) of the centered X-matrix:
where r equals the rank of 
. The singular values are arranged in
descending order:
( 
).
The unit vector 
consists of coefficients for the linear combination
of X-variables with maximal sample variance and the actual sample
variance equals 
. This linear combination is also known
as the first sample principal component. The unit vector 
contains
scaled observations for this linear combination. The second principal
component ( 
) is found by maximizing the sample variance
( 
) of linear combinations orthogonal to 
. The
other components follow successively. PCR estimates the regression
parameters on the basis of the first K components ( 
). Parameters
corresponding to the other components are set to zero. The parameter
estimates in a model with a centered X-matrix can then be written as:
and the OLS solution is obtained when K=r.
PCR and the other single response methods can, of course, be used to
estimate the regression parameters in multiresponse models. Specialized
methods for multiple responses are also developed (see Breiman and
Friedman (1997)). Such methods utilize the inter-relationships between the
response variables. For example, in reduced rank regression (Davies and
Tso, 1982) is restricted to have a specified rank. The least squares
estimation of under reduced rank regression model can be viewed as
a method that replaces the original responses by principal components.
These principal component are constructed from SVD of the original
responses projected onto the X-space. The metods PLS2 (Martens and
N‘s, 1989) and multiresponse ridge regression (Frank and Friedman, 1993)
are designed to handle collinearity in both and 
simultaneously.
In this area I believe that there is a potential for further improvements.
However, for estimation purposes, the major problem is collinearity among
the X-variables since this is most important for prediction error. Therefore
the single response methods are satisfactory in many cases.
When we can design the X-matrix, this matrix is always designed to be as orthogonal as possible (See Table 2 in PAPER 4 for different design criteria). In the single response case, the regression parameters are always estimated by OLS. We may, however, use methods such as reduced rank regression when there are several correlated responses. Many chemometricians would also use PLS2 on such data. In PAPER 2 we show that PLS2 applied to orthogonal explanatory variables is identical to reduced rank regression.
PAPER 4 addresses the problem of testing hypotheses under the regression model. The reasons for not using OLS for estimation are also reasons for not using the traditional test statistics for testing. Moreover, handling collinearity among the responses is much more important for testing than it is for estimation. For this reason ordinary MANOVA has not been as successful as ANOVA. In the future it is important to develop alternative tests that are more powerful in practice. More available data should always result in more information from the statistical analysis. PAPER 4 describes how multivariate tests can be understood geometrically. This paper also outlines principles for calculating Monte Carlo p-values for generalized test statistics. To develop new methods in complex situations, intuitive (e.g. geometrical) understanding is always very important.
A simple method that can improve the ordinary Hotelling 
test in
collinear cases is to replace the original response data by observations
according to the K first principal components. A problem is of course how
to choose K. However, when there are many observations, I believe that
much better methods can be developed.
In variable selection procedures generalized testing techniques can be very useful. PAPER 3 presents some possible tests for the non-orthogonal uniresponse case. This paper focuses mainly on orthogonal design, but it is important that general methods work well in simple special cases. It is also useful that good ideas for simple cases can be extended to general cases.
In two level factorial designs experiments are done at all possible level
combinations. That is 
experiments, where k is the number of
factors. There are always as many parameters as there are level
combinations. The most useful parametrization is based on the ordinary
ANOVA model. We have one constant term and the other parameters are
main effects, two factor interactions and higher order interactions. When no
replicates are done we will have no direct estimate of error, but we can often
assume that higher order interactions are negligible.
Using fractional factorial designs we do not run experiments at all possible level combinations, only at a fraction of them. We can of course not estimate all the parameters, but we can estimate sums of groups of parameters. We say that parameters belonging to the same group are confounded.
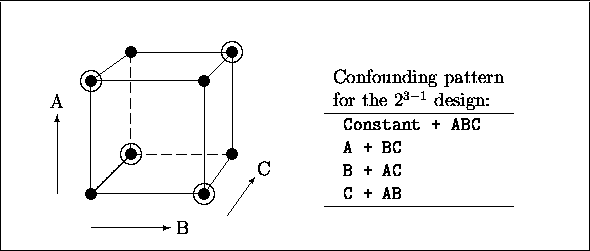
Figure 1:
design and 
design (the four points marked with circles).
Figure 1 shows an example of a design together with its
confounding pattern.
The so-called resolution IV designs have become very popular. In such design no main effects are confounded with other main effects or two factor interactions. If we assume that three factor interactions are negligible, we can estimate each main effect individually. We will, however, seldom have enough degrees of freedom to perform powerful t tests.
Note that the underlying statistical model is a special case of the general regression model where the explanatory variables are orthogonal. For more details on such design, I refer to standard books on experimental designs, such as Box et al. (1978) and Montgomery (1991).
The normal probability plot is the most common way to analyze fractional factorial experiments. It is a very powerful technique because the important factors can be found without any error estimation. However, one needs experience to interpret the plot and therefore an additional and more formal analysis is required.
One such approach is the bayesian approach presented by Box and Meyer (1986, 1993). A disadvantage is that stronger assumptions are needed. The methods are based on calculating posterior probabilities that the true effects are nonzero. One have to assume prior probabilities and prior distributions.
Other alternative methods are based on hypothesis testing. One such method, named COSCIND, is presented in PAPER 1. This paper illustrates probability plotting, bayesian analysis (bayes plot) and COSCIND on data from cheese production. Hypothesis testing techniques can in general be divided into two groups: backward/forward procedures and procedures based on one critical value. An introduction to this topic is given in the introduction of PAPER 3. This paper presents a unified framework for both backward and forward procedures. Below, I give a very brief description to the forward procedure (notation as in PAPER 5).
The n-1 estimated effects, 
, 
, 
, 
, are sorted
according to their absolute values: 
.
The test statistic for the general step number j is
where 
is a chosen number of effects for the denominator ( 
).
The corresponding p-value is calculated under the assumption that the
already selected j-1 effects represent the true relationship. A Monte Carlo
p-value can be found by generating several independent quasi statistics
from the null distribution. To generate a quasi statistic we generate n-j
independent chi-square distributed variables with one degree of freedom. The
statistic is calculated as the largest divided by the mean of the
smallest. The forward procedure stops when a p-value larger than our
significance level is obtained.
The backward procedure is more problematic from a statistical perspective. It is not straight forward to fine the true null distribution. PAPER 3 states and proves a theorem which is important in this case. It is also much more problematic to calculate the error rates in the backward cases (see PAPER 3).
Also note that the methods utilize possible independent degrees of freedom for error (from e.g. center points).
When using the methods mentioned so far we can end up with a model that I will call unrealistic. I do not believe in a model of for example only the interaction term AB. When AB is in the model then the main factors A and B should also be in the model. In section 5 of PAPER 3 we bring in restrictions so that we only search for realistic models. The main reason for introducing these restrictions is, however, to increase the power of the tests. In PAPER 3 the different methods are compared and illustrated on an example from mayonnaise production.
Single response methods may also be used when there are several responses. In many cases this is, however, not satisfactory. One problem is that the experimentwise error rate can grow dramatically since we are performing many individual tests. In some cases there are so many responses that individual analyses are not of interest. Another reason for using multiresponse methodology, is that we can utilize the inter-relationships between the response variables.
One multiresponse approach, which is closely related to PAPER 2, is to perform a principal decomposition of the observed responses. Thereafter, the principal components are treated as single response variables. This can be a very useful method, since we can reduce the number of response variables to be handled.
PAPER 5 presents multiresponse generalizations of the forward procedure
described above. Just as the single response tests can be viewed as a
generalization of the ordinary t tests, the multiresponse tests in PAPER 5
can be viewed as a generalization of the Hotelling test. Moreover,
PAPER 5 presents a further generalization that incorporates successive
principal component decompositions. In this way collinearity among the
responses is effectively handled. It is interesting to note that the test can be
viewed as a double generalization of the ordinary Hotelling test.
Principal component decomposition (of responses) and variable selection (of
explanatory variables) is treated simultaneously. In PAPER 5, the
methodology is illustrated with an example from baguette production.
Identifying Significant Effects in
Fractional
Factorial Single- and
Multi-response
Experiments
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 -no_navigation thesis.
The translation was initiated by Øyvind Langsrud on Wed Dec 3 13:24:18 MET 1997
